VAE on Hilbert Spaces to generate functional data

Generative models are attracting a lot of attention partly because of their ability to learn from cheap unlabelled data. Instead of learning to discriminate between categories or performing regression tasks, this class of models learns to generate synthetic samples with the same properties as the input data $ \mathbf{X} $ . More specifically a generative model aims to learn the distribution $ p(\mathbf{X}) $ which the input data originates from. This enables us to understand the distribution of the data, synthesise data from this distirbution, and perform tasks such as:

• Augmenting data sets for better model generalisation
• Out of distribution detection
• Density estimation

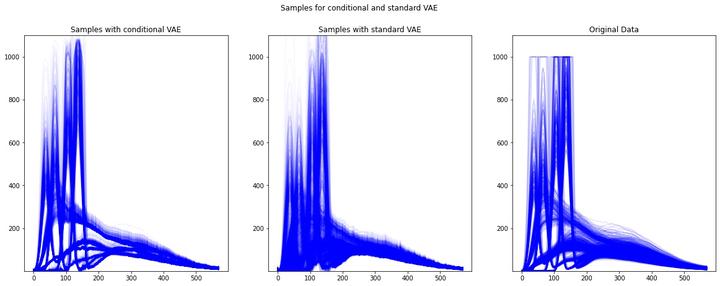
While deep learning and generative models have lead to many successes partly because of advances in available data and computational resources, we have also seen a big step in data collection methods. The increasing amount of high frequency data arising from fields such as finance and medicine motivates the perspective of functional data analysis (FDA). The central assumption of FDA is that observations are treated as discretised functions rather than multivariate vectors. This approach leads to several advantages especially when the observations contain many function evaulations (i.e. very high dimensional vectors).

Motivated by these two observations, I explored the applicability of Variational Autoencoders to functional data by representing the functional data in a basis. My full thesis can be downloaded here and slides for the talk here.